C++ OpenCV系统学习——图像阈值操作、线性滤波
目录
1.概念
1.1图像阈值(threshold)
1.2阈值类型——阈值二值化(threshold binary)
1.3 阈值类型——截断(truncate)
1.4阈值类型——阈值取零(threshold to zero)
1.5阈值类型——阈值反取零(threshold to zero inverted)
2.线性滤波
2.1卷积概念
2.1.1卷积的原理
3.自定义卷积模糊
1.概念
1.1图像阈值(threshold)
阈值简单的来说就是图像分割的标尺,这个标尺是如何产生的,阈值的产生算法是什么,阈值类型?
1.2阈值类型——阈值二值化(threshold binary)
左下方的图表示图像像素点Src(x,y)值分布情况,蓝色水平线表示阈值
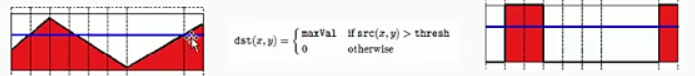
1.3 阈值类型——截断(truncate)
左下方的图表示图像像素点Src(x,y)值的分布情况,蓝色水平线表示阈值

1.4阈值类型——阈值取零(threshold to zero)
左下方的图表示图像像素点Src(x,y)值的分布情况,蓝色水平线表示阈值

1.5阈值类型——阈值反取零(threshold to zero inverted)
左下方的图表示图像像素点Src(x,y)值的分布情况,蓝色水平线表示阈值

2.线性滤波
2.1卷积概念
-
卷积是图片处理中的一个操作,是kernel在图片的每个像素上的操作
-
kernel本质上是一个固定大小的矩阵数组,其中心点称为锚点
2.1.1卷积的原理

卷积核也成为卷积算子,比较常见的算子有:

利用Robert算子分别从X和Y方向滤波结果如下:
void MyApi::linear_filter(Mat & image)
{
Mat x_dst;
//Robert X方向
Mat kerner_x = (Mat_<int>(2, 2) << 1, 0, 0, -1);
filter2D(image, x_dst, -1, kerner_x, Point(-1, -1), 0.0);
//Robert Y方向
Mat y_dst;
Mat kerner_y = (Mat_<int>(2, 2) << 0, 1, -1, 0);
filter2D(image, y_dst, -1, kerner_y, Point(-1, -1), 0.0);
namedWindow("Robert_x", WINDOW_FREERATIO);
imshow("Robert_x", x_dst);
namedWindow("Robert_y", WINDOW_FREERATIO);
imshow("Robert_y", y_dst);
}
 我们可以看到在x和Y方向的梯度
我们可以看到在x和Y方向的梯度
Sobel算子:
void MyApi::linear_filter(Mat & image)
{
Mat x_dst;
//Robert X方向
Mat kerner_x = (Mat_<int>(2, 2) << 1, 0, 0, -1);
filter2D(image, x_dst, -1, kerner_x, Point(-1, -1), 0.0);
//Robert Y方向
Mat y_dst;
Mat kerner_y = (Mat_<int>(2, 2) << 0, 1, -1, 0);
filter2D(image, y_dst, -1, kerner_y, Point(-1, -1), 0.0);
//Sobel算子X方向
Mat sobel_x_dst;
Mat sobel_kerner_x = (Mat_<int>(3, 3) <<-1,0,1,-2,0,2,-1,0,1);
filter2D(image, sobel_x_dst, -1, sobel_kerner_x, Point(-1, -1), 0.0);
//Sobel算子Y方向
Mat sobel_y_dst;
Mat sobel_kerner_y = (Mat_<int>(3, 3) << -1, -2, -1, 0, 0, 0, 1, 2, 1);
filter2D(image, sobel_y_dst, -1, sobel_kerner_y, Point(-1, -1), 0.0);
namedWindow("Robert_x", WINDOW_FREERATIO);
imshow("Robert_x", x_dst);
namedWindow("Robert_y", WINDOW_FREERATIO);
imshow("Robert_y", y_dst);
namedWindow("Sobel_x", WINDOW_FREERATIO);
imshow("Sobel_x", sobel_x_dst);
namedWindow("Sobel_y", WINDOW_FREERATIO);
imshow("Sobel_y", sobel_y_dst);
}

Laplace算子类似操作就不写了。Laplace算子可以获取整个的轮廓结果
3.自定义卷积模糊
前面我们使用了常见的算子进行卷积,我们也可以自定义卷积:
filter2D方法filter2D(
Mat src,
Mat dst,
int depth//深度不知道就默认-1,
Mat kernel,
Point anchor,//锚点位置就默认Potin(-1,-1)
double delta//计算出来的像素+delta
)
其中kernel是可以自定义的卷积核
案例:自定义算子:完成模糊逐渐加深,每过0.5s就加深模糊一次,只有按ESC键才会结束
void MyApi::linear_filter(Mat & image)
{
//Mat x_dst;
Robert X方向
//Mat kerner_x = (Mat_<int>(2, 2) << 1, 0, 0, -1);
//filter2D(image, x_dst, -1, kerner_x, Point(-1, -1), 0.0);
Robert Y方向
//Mat y_dst;
//Mat kerner_y = (Mat_<int>(2, 2) << 0, 1, -1, 0);
//filter2D(image, y_dst, -1, kerner_y, Point(-1, -1), 0.0);
Sobel算子X方向
//Mat sobel_x_dst;
//Mat sobel_kerner_x = (Mat_<int>(3, 3) <<-1,0,1,-2,0,2,-1,0,1);
//filter2D(image, sobel_x_dst, -1, sobel_kerner_x, Point(-1, -1), 0.0);
Sobel算子Y方向
//Mat sobel_y_dst;
//Mat sobel_kerner_y = (Mat_<int>(3, 3) << -1, -2, -1, 0, 0, 0, 1, 2, 1);
//filter2D(image, sobel_y_dst, -1, sobel_kerner_y, Point(-1, -1), 0.0);
//namedWindow("Robert_x", WINDOW_FREERATIO);
//imshow("Robert_x", x_dst);
//namedWindow("Robert_y", WINDOW_FREERATIO);
//imshow("Robert_y", y_dst);
//namedWindow("Sobel_x", WINDOW_FREERATIO);
//imshow("Sobel_x", sobel_x_dst);
//namedWindow("Sobel_y", WINDOW_FREERATIO);
//imshow("Sobel_y", sobel_y_dst);
//自定义算子:完成模糊逐渐加深,每过0.5s就加深模糊一次
Mat dst;
int c = 0;
int index = 0;
int ksize = 0;
while (true)
{
c = waitKey(500);
if ((char)c == 27)//当按ESC键跳出
{
break;
}
ksize = 4 + (index % 5) * 2 + 1;
Mat kernel = Mat::ones(Size(ksize, ksize), CV_32F / (float)(ksize * ksize));
filter2D(image, dst, -1, kernel, Point(-1, -1));
index++;
namedWindow("自定义算子", WINDOW_FREERATIO);
imshow("自定义算子", dst);
}
}
————————————————
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/bigData1994pb/article/details/119347936